Measuring Star Distance with Parallax: The Cosmic Ruler

Look up at the night sky. What do you really see?

It’s a beautiful, glittering tapestry. It looks… flat. Like a black ceiling with a bunch of tiny lights poked through it. We even talk about constellations like Orion or the Big Dipper as if they’re 2D drawings, as if all those stars are pasted at the same distance.

But you know that’s not true, don’t you? Your gut knows the universe has depth. Some of those stars are our neighbors, practically next door. Others are so far away it’s hard to even think about.

But how do we know? How do we prove it?

You can’t exactly run a cosmic tape measure out to Betelgeuse. You can’t bounce a laser off Proxima Centauri and time the return trip. The distances are just… staggering. They break our everyday intuition. For centuries, this was one of the single biggest questions in all of science: How far away are the stars?

The answer, it turns out, is a trick. A simple geometric trick, one you can try right now, this very second. It’s the fundamental tool for measuring star distance with parallax. This method is the first, most critical rung on what astronomers call the “Cosmic Distance Ladder,” a set of tools that lets us measure the entire, observable universe.

More in The Observer’s Sky Category

Where to See a Planetary Conjunction

When to See Planetary Opposition

Key Takeaways

If you only remember a few things from this whole article, make ’em these:

• Stellar Parallax: This is just the fancy term for a star’s apparent shift in position as we orbit the Sun. A nearby star will look like it’s in a different spot in July than it was in January, all against a background of super-distant, “fixed” stars.
• The Only Direct Method: This is critical. Parallax is the only way we have to measure star distances directly with geometry. Every other method, for every other object, has to be calibrated using this one first.
• The Magic Formula: It’s beautifully simple. The parallax angle (we’ll call it p) and the distance (d) are just an inverse of each other: d = 1/p. A tiny angle means a huge distance.
• The “Parsec”: You hear this all the time. It’s the unit astronomers actually use, and it was invented specifically for this. It literally means “parallax-second.”
• Space is the Place: Trying to do this from Earth is a nightmare because of our atmosphere. The real breakthroughs came from space missions like ESA’s Hipparcos and the modern game-changer, Gaia, which is mapping billions of stars.

What Exactly Is This “Parallax” You’re Talking About?

That word itself, “parallax,” might sound technical. A little intimidating. But I promise you, the concept is something you use every single second of every single day.

It’s built into your brain. It’s the whole reason you have two eyes.

Parallax is, simply, the apparent shift in an object’s position when you look at it from two different locations.

Your brain is a parallax machine. It constantly compares the slightly different image from your left eye with the slightly different image from your right eye. It mashes them together, and bam—depth perception. It’s how you can tell, without thinking, that your coffee cup is within reach but the door is across the room.

Can You Give Me a Simple, Everyday Example?

You bet. Let’s do it right now.

Go on, hold your thumb out at arm’s length.

Now, close your right eye. Just use your left eye to look at your thumb and line it up with something in the background. A light switch, a picture on the wall, a tree outside the window. Got it?

Okay, don’t move your thumb. Don’t move your head. Just close your left eye and open your right eye.

What happened?

Your thumb “jumped,” didn’t it? It’s nowhere near that background object anymore. It looks like it just hopped to the side.

That’s it. That is parallax.

Your thumb didn’t move. The wall didn’t move. But by changing your viewpoint (from your left eye to your right eye), your thumb’s apparent position against that distant background changed. The distance between your two “viewpoints” (your eyes) is what we call the baseline. The “jump” you just saw is the parallax shift.

How Do We Take That Thumb Trick into Space?

So, we can measure the distance to our thumb. Fantastic. How do we scale that up to a star?

We need two things. A much bigger baseline. And a much more distant background.

What’s Our “Baseline” for Stargazing?

The baseline between our two eyes is just a few inches. That’s great for seeing depth in a room, but it’s totally useless for stars. The stars are so far away that even if you had one eye on one side of the Earth and one on the other—an 8,000-mile baseline—the stars still wouldn’t appear to move. Not one bit.

So, astronomers needed the biggest baseline they could possibly get. What’s the biggest motion we have available?

Our entire planet’s orbit around the Sun.

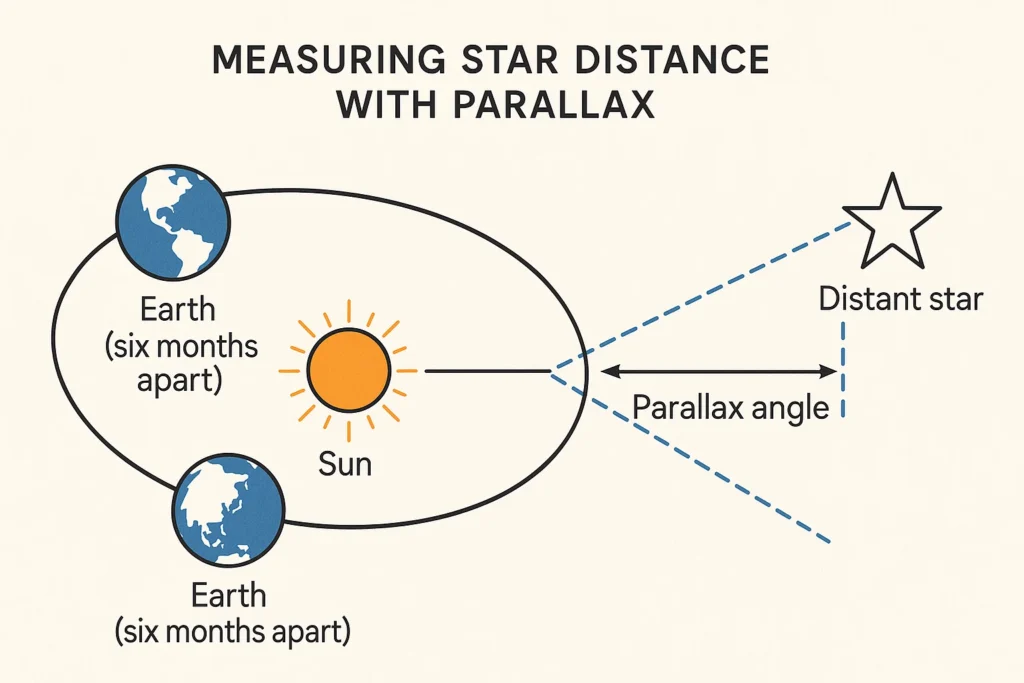
Here’s the plan: We take a picture of a star we think is “nearby.” We’ll do it in January. We carefully, meticulously, note its position against all the other, fainter stars in the background.

Then, we wait.

We wait six months. In July, the Earth has traveled all the way to the exact opposite side of its orbit. We are now separated from our January position by about 186 million miles (300 million kilometers). That is our new baseline.

Now, we take a second picture of that same star.

And just like your thumb, that star will have moved. It will have “jumped” slightly against the background of much, much more distant stars.

So, the Star “Jumps” Against… What?

This is a perfectly logical question. If all the stars are moving, how can you measure one moving against the others? Aren’t the background stars “jumping” too?

The key here is the sheer, mind-numbing scale of the universe.

The stars we measure with parallax are our “nearby” neighbors. They might be 10, 50, or 1,000 light-years away. But the “background” stars we use for reference? They are tens of thousands or hundreds of thousands of light-years away. Or they might even be entire other galaxies that just look like faint smudges.

Compared to our target star, these background objects are so colossally far away that they are, for all intents and purposes, fixed. They don’t move. They are the “distant mountains” in our thumb analogy. The parallax shift of our “nearby” target star is small, but measurable. The parallax shift of the background stars is so tiny it’s basically zero.

This tiny, measured shift is called the stellar parallax angle. We usually write it as p. (Technically, it’s half of the total shift we see over the six months, forming a tall, skinny triangle).

This Sounds Simple. Why Was It So Hard to Do?

The logic is dead simple, right? A kid could get it.

The execution, however, is agonizingly difficult. For centuries, the greatest astronomers on Earth—geniuses—tried to measure stellar parallax and failed. Every single one of them.

Their failure was actually used as “proof” that the Earth didn’t move. Think about it: if the Earth orbits the Sun (the Copernican idea), the stars must show parallax. The ancient Greeks, like Aristarchus of Samos, figured this out. But nobody could see it. No matter how hard they looked, they saw no shift.

This led them to two possible conclusions:

1. The Earth is stationary at the center of the universe. The geocentric model is correct.
2. The Earth does move, but the stars are so mind-bogglingly, absurdly far away that the shift is too small to be seen with the human eye or early telescopes.

Faced with those two options, which one would you choose? They chose the first. It just seemed far more likely. The second option implied a universe of a size that was terrifying and just felt ridiculous.

As it turns out, the ridiculous answer was the right one.

Just How Small Are These Angles We’re Measuring?

The angles are small.

No, smaller than that.

They are microscopic.

We measure angles in degrees. You know this. A full circle has 360 degrees. If you hold your little finger out at arm’s length, its width covers about 1 degree of the sky. The full Moon is about half a degree.

This unit is way, way too big for our purposes.

We have to divide that 1-degree slice into 60 smaller units. We call those arcminutes. The full Moon is about 30 arcminutes wide.

Still too big.

We then have to divide one of those tiny arcminutes into 60 even smaller units. These are called arcseconds. So, one single arcsecond is 1/3600th of one single degree.

This is the unit of parallax.

How small is one arcsecond? It’s the apparent size of a dime seen from 2.5 miles (4 km) away. It’s the width of a single human hair seen from 65 feet (20 meters) away.

And that is the “jump” astronomers were trying to measure.

To put it in perspective, the nearest star to us, Proxima Centauri, has the largest parallax of any star: a “massive” 0.77 arcseconds. Less than one.

Who Finally Cracked the Code?

For centuries, astronomers built better and better telescopes, all chasing this holy grail. Measuring parallax was more than just finding a distance. It would, at a stroke, prove that Copernicus was right, that the Earth moved, and it would give us the first true scale of the cosmos.

The race was finally won in 1838. The man who did it was a German astronomer named Friedrich Bessel.

He was clever. He didn’t just aim for the brightest star in the sky (a mistake others had made). He aimed for a smart target. He chose a faint star in the constellation Cygnus called 61 Cygni.

Why that one? Because it had a very high “proper motion.” That means it was visibly streaking across the sky (relative to other stars) very quickly from year to year. Bessel reasoned, correctly, that a star moving that fast was like a person walking quickly past your car window—they must be nearby.

After months and months of painstaking, frustrating observations, Bessel announced his result. He had measured the parallax of 61 Cygni. The angle was 0.314 arcseconds.

It was a tiny, tiny number. But it was one of the most profound measurements in human history. The stars were not lights on a crystal sphere. The universe was deep. And for the very first time, we had a ruler.

Bessel wasn’t totally alone, by the way. In that same era, Thomas Henderson measured the parallax of Alpha Centauri (though he published his results a bit later) and Friedrich Struve measured Vega. The floodgates were open.

Let’s Talk Units. What’s a “Parsec” and Why Do Astronomers Use It?

Okay, so Bessel measured an angle of 0.314 arcseconds. Great. What does that mean for the distance? How many miles is that?

This brings us to the wonderfully simple math of parallax and the unit that astronomers invented specifically for it. Forget miles. Forget kilometers.

Is “Parsec” Short for Something?

Yes. It’s a portmanteau. It’s a smush-word for “parallax-second.”

The definition is built right into the name. Astronomers defined a new unit of distance, the parsec, with this elegant idea:

A parsec is the distance a star would be if it had a parallax angle of exactly 1 arcsecond.

This is ingenious. It’s not just clever; it’s practical. It directly links the thing they measure (arcseconds) to the result they want (distance) with the simplest possible math.

So How Does the Math Work?

Using some basic high school trigonometry (the “small angle approximation,” if you’re curious), the relationship is beautiful. The distance to a star (in parsecs) is simply the inverse of its parallax angle (in arcseconds).

The formula is: d = 1/p

That’s it. That’s the whole thing.

Let’s use Bessel’s star, 61 Cygni, as an example.

• Its parallax (p) was 0.314 arcseconds.
• Its distance (d) = 1 / 0.314
• d ≈ 3.18 parsecs.

Done. Let’s try our nearest neighbor, Proxima Centauri.

• Its parallax (p) is 0.77 arcseconds.
• Its distance (d) = 1 / 0.77
• d ≈ 1.3 parsecs.

You can see why astronomers love this. No complex trig needed for the final step. You measure the tiny angle in arcseconds, you hit the 1/x button on your calculator, and you have the distance in parsecs.

How Does This Compare to a Light-Year?

We hear “light-year” all the time in movies and pop science. A light-year is also a unit of distance, not time. It’s simply the distance light travels in one year. It’s a very poetic and intuitive concept.

So how do they relate?

One parsec is equal to about 3.26 light-years.

So, Proxima Centauri is about 1.3 parsecs away, which is also about 4.24 light-years away. Both are correct. Astronomers just tend to use parsecs (and kiloparsecs—thousands of parsecs) because it comes directly from their primary measurement method: measuring star distance with parallax.

What’s Stopping Us from Measuring Every Star This Way?

Okay, we’ve got the method. We’ve got the math. We’ve got the units. Why don’t we just measure the parallax of all 100 billion stars in our galaxy and call it a day?

Well, we ran face-first into two colossal, show-stopping problems: our own atmosphere and the simple, brutal tyranny of distance.

Why Can’t We Just Use Our Backyard Telescopes?

The single biggest enemy of any ground-based astronomer is the very air we breathe. It’s ironic, isn’t it?

The atmosphere is not a calm, clear, perfect window. It’s a turbulent, swirling ocean of air. Pockets of warm and cold air are constantly rising and falling, and they act like tiny, messy, imperfect lenses.

This is what causes stars to “twinkle.”

Twinkling might be pretty for poets, but for an astronomer, it’s a nightmare. It blurs, distorts, and makes the tiny, pinprick image of a star dance around like a drunken firefly. This atmospheric blurring even has a name: “seeing.”

Now, imagine trying to measure an angle that’s the size of a dime 2.5 miles away… while you’re looking at it from the bottom of a swimming pool, with the water churning.

That’s ground-based parallax measurement.

For decades, this “atmospheric wall” was unbeatable. It limited us. We could only get reliable parallax measurements for a few thousand of the very closest stars—those within about 100 parsecs (around 300 light-years). Beyond that, the parallax angle became smaller than the atmospheric blurring. The tiny “jump” was completely lost in the “twinkle.” We were stuck.

The Tyranny of Distance: An Unbeatable Foe?

The other problem is that elegant formula: d = 1/p. It’s a curse as much as a blessing.

It means that as the distance (d) gets bigger, the parallax angle (p) gets smaller. And it gets smaller fast.

• A star at 10 parsecs has p = 0.1 arcseconds. (This is very hard, but just barely doable from the ground on a perfect night).
• A star at 100 parsecs has p = 0.01 arcseconds. (This is at the absolute, theoretical limit of ground-based tech).
• A star at 1,000 parsecs has p = 0.001 arcseconds. (This is a milliarcsecond. Forget it. It’s impossible from the ground).

Our Milky Way galaxy is about 30,000 parsecs across. If we could only measure out to 100 parsecs… we were effectively blind. We had a ruler that could measure our front yard, but we lived in a country the size of North America.

We were stuck.

How Did We Break Past This “Parallax Wall”?

If the problem is that you’re at the bottom of a churning swimming pool, what’s the solution?

Get out of the pool.

If the problem is the Earth’s atmosphere, the solution is just as obvious (though way more expensive): you have to get above it. We had to send a telescope into space.

Enter Hipparcos: The First Eye in the Sky

In 1989, the European Space Agency (ESA) launched a revolutionary satellite. Its name was Hipparcos (which stood for High Precision Parallax Collecting Satellite). It was a great name, honoring the ancient Greek astronomer Hipparchus, who created the first great star catalog.

Floating in the black, freed from the shimmering, blurring atmosphere, Hipparcos could measure angles with a precision of about 0.001 arcseconds. One milliarcsecond.

From 1989 to 1993, this little satellite patiently scanned the sky, measuring the positions and parallaxes of 118,000 stars.

The result was the Hipparcos Catalogue, released in 1997. It was a thunderclap in the world of astronomy. It instantly increased the number of stars with accurate distances by a factor of 100. It pushed that “parallax wall” back from 100 parsecs to 1,000 parsecs.

For the first time, we had a solid, reliable 3D map of our entire local stellar neighborhood. For 20 years, it was the gold standard.

Is Hipparcos Still the King? (Spoiler: Not Even Close.)

Hipparcos was a revolution. It changed everything.

But what came next… well, what came next was an extinction-level event for our old maps of the sky.

If Hipparcos was a revolution, the Gaia mission is something else entirely. It’s a total re-writing of the rulebook.

The New Standard: Why is Everyone Talking About ‘Gaia’?

Also an ESA mission, Gaia was launched in 2013 and is still up there, scanning the sky relentlessly. Its goal is simple and just… breathtaking: to create the most precise and extensive 3D map of our Milky Way galaxy ever made.

Let’s compare. Hipparcos measured 118,000 stars. Gaia is measuring more than 1.8 billion stars.

This isn’t just an upgrade. It’s not like getting a new iPhone. It’s like going from a horse and buggy to a warp-drive starship.

Gaia is measuring so many stars, with such precision, that its data map doesn’t just show our little neighborhood. It reveals the entire structure of our galaxy—the spiral arms, the central bar, the ghostly halo of stars surrounding it all.

What Kind of Insane Precision Does Gaia Have?

Gaia’s precision is difficult to put into words. It measures angles in microarcseconds. That’s one-millionth of an arcsecond.

Let’s go back to our analogies.

• An arcsecond was a dime seen from 2.5 miles away.
• A milliarcsecond (Hipparcos) was that same dime seen from 2,500 miles away (the distance from L.A. to New York).
• A microarcsecond (Gaia) is the equivalent of measuring the width of a human hair… as seen from the Moon.

It’s… absurd. The precision is so profound that the system has to account for things like the tiny bending of starlight caused by the gravity of Jupiter as it moves around the Sun. It even has to account for Albert Einstein’s general relativity and the way spacetime itself is warped.

What Can We Do With Gaia’s Data?

With this power, Gaia is extending our parallax ruler out to 10,000 parsecs (over 30,000 light-years). That’s a huge chunk of the entire galaxy.

But here’s the real kicker. Gaia doesn’t just measure a star’s position once. It scans the sky over and over and over. So it doesn’t just get a static 3D snapshot. It gets a 6D map. It measures:

1. 3D Position (where it is)
2. 3D Motion (where it’s going)

It tracks the “proper motion” (sideways drift) and the “radial velocity” (movement toward or away from us) for billions of stars.

We can literally watch our galaxy in motion. We can see streams of stars that were torn from other, smaller galaxies that our Milky Way “ate” billions of years ago. We can see how the spiral arms rotate. We can trace the orbits of stars, running them backward in time to see where they were born and forward to see where they will die.

It is, without a single shred of exaggeration, the most important dataset in modern astronomy. And all of it, every last bit, is built on that one simple, fundamental principle: parallax.

Why Do We Care So Much About Distance? Isn’t “Far” Good Enough?

This is the real “so what?” question, isn’t it? Okay, we know Star A is 100 light-years away and Star B is 120 light-years away. Who cares?

We care because distance is the “Rosetta Stone.” It’s the key that unlocks everything else about a star.

The “Luminosity” Problem: Is That Star Bright or Just Close?

Imagine you’re standing on a dark road. You see two lights. One is a dim flashlight, but it’s only 10 feet away. The other is a brilliant, blinding searchlight, but it’s 10 miles away.

Which one looks brighter to your eye?

The flashlight, of course.

This is the “apparent brightness” problem. When we look up at a star, all we see is its apparent brightness. We have no idea if it’s a dim little flashlight that’s very close, or a cosmic searchlight that’s very, very far away.

This is the single most important takeaway: Without knowing the distance, you cannot know a star’s true brightness.

But once you have the distance (thanks, parallax!), you can correct for it. You can do the math and calculate what astronomers call its absolute luminosity—its true, intrinsic power. You can finally know if you’re looking at a flashlight or a searchlight.

How Does Knowing Distance Unlock a Star’s Secrets?

Once you have a star’s absolute luminosity, the floodgates open. You can finally stop guessing and start doing real physics.

Knowing a star’s true brightness (and its color, which tells you its temperature) allows astronomers to figure out all its other properties:

• Its Size (Radius): A hot, bright star must be enormous. A cool, bright star must be even more enormous (a red giant). A hot, dim star must be tiny (a white dwarf).
• Its Mass: This is a big one. By finding stars in binary systems (two stars orbiting each other) and knowing their distance, we can use Kepler’s laws of motion to calculate their mass.
• Its Age & Evolution: This is the most beautiful part. When you plot thousands of stars on a graph of their true luminosity vs. their temperature, they don’t just fall randomly. They fall into distinct patterns—a long line called the “main sequence,” a cluster called the “giant branch,” and so on. This is the famous Hertzsprung-Russell (H-R) diagram. It’s not just a graph; it’s a direct snapshot of how stars are born, how they live, and how they die.

That H-R diagram, the single most powerful tool for understanding the lives of stars, cannot exist without parallax. Parallax is what gives you the “Luminosity” (vertical) axis of the graph.

Is Parallax the Only Ruler We Have?

Yes… and no.

Parallax is the only direct method. It’s the only one that relies on pure, unadulterated geometry. It makes no assumptions about the star’s physics. It is the gold standard. It is the ruler.

But as we’ve seen, even with Gaia, it has its limits. We can’t use parallax to measure a star in the Andromeda galaxy, which is 2.5 million light-years away. The angle is just too impossibly small.

So what do we do? We build a “ladder.”

The First Rung: Why Parallax is the “Cosmic Distance Ladder”

Think of parallax as the first, most solid, most trustworthy rung on a very, very tall ladder. It’s the one touching the ground.

We use our parallax ruler to measure the distance to every single object we can reach within our own galaxy. This includes not just normal stars, but also a few very special types of “standard candle” stars.

How Do We Calibrate Rulers for Deeper Space?

The most famous “standard candles” are called Cepheid Variable Stars. These are special, pulsating giant stars. In the early 1900s, an astronomer named Henrietta Leavitt discovered a remarkable, clockwork-like property: the period of their pulsation (how long it takes them to get bright, dim, and bright again) is directly related to their absolute luminosity.

This is a cosmic gift. A star that pulses every 50 days is intrinsically brighter than one that pulses every 5 days.

But how did we figure out that exact relationship? Simple:

1. First, we found a bunch of Cepheid variable stars close enough to us in our own galaxy (and its little satellite galaxies, the Magellanic Clouds).
2. Then, we measured their distance with parallax (using Hipparcos and now Gaia).
3. Since we had the distance, we could calculate their true absolute luminosity.
4. Finally, we plotted their true luminosity against their pulsation period and created a rock-solid calibration chart.

Now we’re ready. We can find a single Cepheid variable star in a distant galaxy, millions of light-years away. We can’t measure its parallax. It’s too far. But we can measure its period. We just watch it for a few weeks. We see it pulses every 10.3 days.

We look at our parallax-calibrated chart and say, “Aha! A 10.3-day period means it has an absolute luminosity of X.” We then compare that true brightness to its apparent brightness (how dim it looks in our telescope). The difference tells us the distance.

This is exactly how Edwin Hubble first measured the distance to the Andromeda galaxy. It’s how we measure the distances to other galaxies. And that, in turn, is how we discovered the expansion of the universe itself.

Every single measurement of cosmic scale—the size of galaxies, the distance to quasars, the age of the universe—all of it rests on the “Cosmic Distance Ladder.”

And the very first, most fundamental, load-bearing rung of that entire ladder is, and always will be.

What’s Next? Can We Get Even Better?

For now, the astronomical world is still drinking from the firehose of data that is the Gaia mission. Its data releases (the third big one was in 2022) are so vast and precise that astronomers will be mining them for decades to come. A whole generation of science is being built on that foundation.

Future space-based observatories, like the James Webb Space Telescope, don’t measure parallax themselves. Instead, they use Gaia’s perfect distance data to better understand the physics of the objects they study. When JWST looks at a star, it knows how far away it is, so it can know its true properties.

Other future missions might use new techniques, like infrared interferometry, to push the boundaries even further, maybe even peering through the thick dust of the galactic center.

But for the foreseeable future, Gaia is the standard. It is the pinnacle of what that simple, “thumb-trick” concept can achieve.

From a simple observation you can make in your living room, we have built a ruler that can map a billion-star galaxy. The next time you look up at that flat, starry sky, remember that you are looking out into a vast, 3D ocean.

And for the first time in human history, we finally have the chart.

FAQ – Measuring Star Distance with Parallax